应用题,即用语言或文字叙述有关事实,反映数量关系,并求解未知条件的题目。这里主要讲解小学数学学习中常见的三种应用题题型:和差问题、和倍问题、差倍问题。
工具/原料
纸、笔等学习用具
和差问题
1
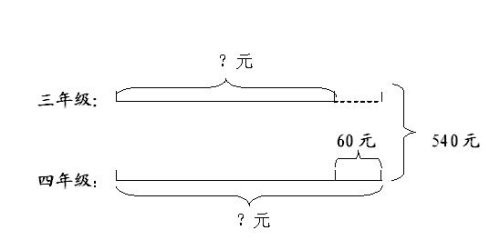
和差问题,是指已知大小两个数的和与它们的差,求这两个数各是多少的应用题。
基本思路:
由于和差问题中的两个数不相同,因此可以用假设的方法使两个数变成相等的数。首先,我们可以先根据题意判断应该怎样假设,一般可假设要求的两个或几个未知数相等,然后根据所作的假设,注意数量关系发生了什么变化,怎样从所给的条件与变化了的数量关系的比较中作出适当的调整,从而求出正确答案。
解题公式:
较大数=(和+差)÷2
较小数=(和-差)÷2

2
例题 1
果园里有苹果树和梨树共420棵,苹果树比梨树多36棵,两种树各有多少棵?
分析:
根据题意可知,假如增加36棵梨树,梨树的棵数就和苹果树的棵数同样多了。但如果增加36棵梨树,苹果树和梨树的总数量就是420+36=456(棵),用456÷2=228(棵)就是果园里苹果树的数量。知道了苹果树的数量,就能很方便地求出梨树的数量了。
故解答过程为:
(420+36)÷2=228(棵)
228-36=192(棵)
答:果园里有苹果树228棵,梨树192棵。
3
例题 2
老师把140块糖分给一班和二班。如果从一班拿12块糖给二班,那么两个班分得的糖就一样多。求原来一班和二班各分得多少块糖?
分析:
根据题意可知,一班减少12块糖,二班增加12块糖后,两个班分得的糖就一样多,就是说一班比二班多分得12×2=24(块)糖。假如从140块糖中去掉24块,剩下的糖就是二班分得糖的2倍,由此先求出二班分得的块数,再求出一班分得的块数。
故解答过程为:
(140-12×2)÷2=58(块)
140-58=82(块)
答:一班分得82块,二班分得58块。
4
例题 3
两箱零件共102个。从甲箱拿出24个放入乙箱后,甲箱还比乙箱多4个。原来两箱各有多少个零件?
分析:
先求出原来甲、乙两箱零件数量的差。因为甲箱减少24个,乙箱增加24个后,甲箱还比乙箱多4个,所以原来甲箱比乙箱多24×2+4=52(个)零件。假如甲箱减少52个零件,则甲、乙两箱的零件就同样多,即(102-52)相当于乙箱零件个数的2倍,由此求出乙箱零件的个数,再求甲箱零件的个数。
故解答过程为:
(102-24×2+4)÷2=25(个)
102-25=77(个)
答:原来甲箱有77个零件,乙箱有25个零件。
5
例题 4
学校三个运动队共有队员80人。已知田径队人数比足球队和篮球队人数的和还多8人,足球队人数又比篮球队多4人。三个队各有多少人?
分析:
根据题意可得,田径队人数比其他两队人数的总和多8人,假设篮球、足球两队人数再增加8人,那么三队的总人数是80+8=88(人),这个人数正好是田径队人数的2倍,因此田径队的人数是88÷2=44(人),篮球队和足球队共有
80-44=36(人)。再根据“足球队人数比篮球队多4人”来假设篮球队增加4人,则足球队的人数就是(36+4)÷2=20(人),用(36-20)来求出篮球队人数。
故解答过程为:
田径队人数:(80+8)÷2=44(人)
足球队人数:(80-44+4)÷2=20(人)
篮球队人数:80-44-20=16(人)
答:学校田径队有44人,足球队有20人,篮球队有16人。
6
练习题:
1、学校买回故事书和科技书共106本,其中故事书比科技书多24本。两种书各买了多少本?
2、两个班共有学生92人,如果从一班调2人到二班,则两班人数同样多。两个班原来各有多少名同学?
3、甲、乙两筐水果共重40千克。从甲筐取6千克放到乙筐后,甲筐里的水果比乙筐还多2千克。求两筐原有水果多少千克?
4、红花、绿花和黄花共有78朵。红花和绿花的总朵数比黄花多6朵,红花比绿花多6朵。三种花各有多少朵?
END和倍问题
1
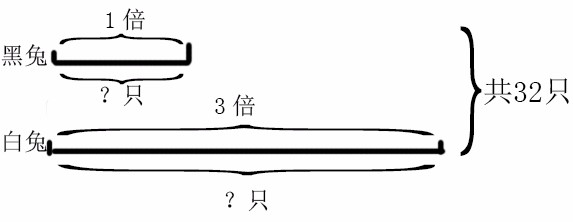
已知两个数的和以及它们之间的倍数关系,求这两个数各是多少的应用题叫做和倍问题。
基本思路:
首先要弄清几个问题:两个数相比,以被比的数为标准,这个被比的数称为一倍数,比的数里有几个这样的一倍数,就是几倍数,我们就说一个数是另一个数的几倍。它们之间的数量关系式是:
一倍数×倍数=几倍数
几倍数÷一倍数=倍数
几倍数÷倍数=一倍数
在解决和倍问题时,先要确定一个数为标准(通常以较小的数为标准),即一倍数,再根据较大的数与较小的数之间的倍数关系,确定总和相当于一倍数(较小的数)的多少倍,然后求出一倍数(较小的数),再算出其他各数。
解题公式:
和÷(倍数+1)=一倍数(即较小的数)
和-较小的数=较大的数 或 较小的数×倍数=较大的数

2
例题 1
小明和小红共有图书84本,小明的图书本数是小红的3倍。小明和小红各有图书多少本?
分析:
由题意可得,小明图书本数是小红的3倍,那么把小红的图书本数看作1份,小明就有这样的3份,总本数84本占了1+3=4份,把84本平均分成4份,1份就是小红的图书本数,3份就是小明的图书本数。
故解答过程为:
84÷(1+3)=21(本)
84-21=63(本) 或 21×3=63(本)
答:小明有图书63本,小红有图书21本。
3
例题 2
果园里有梨树、苹果树、桃树共207棵,其中梨树的棵数是苹果树的3倍,苹果树的棵数是桃树的2倍。三种果树各有多少棵?
分析:
把桃树的棵数看作1份,苹果树的棵数就是这样的2份,梨树的棵数就是桃树的2×3=6倍,三种果树的总棵数就是桃树的6+2+1=9倍。可以先求出桃树有207÷9=23(棵),苹果树有23×2=46(棵),梨树有46×3=138(棵)。
故解答过程为:
207÷(2×3+2+1)=23(棵)
23×2=46(棵)
46×3=138(棵)
答:梨树有138棵,苹果树有46棵,桃树有23棵。
4
例题 3
两箱零件共有88个,如果从甲箱取出15个零件到乙箱,那么乙箱零件数量是甲箱的3倍。两箱原来各有零件多少个?
分析:
从甲箱取出15个零件放入乙箱后,两箱零件的总数没有变,它相当于甲箱的
3+1=4倍,这时甲箱有零件88÷4=22(个),那么甲箱原有零件22+15=37(个),乙箱原有零件88-37=51(个)。
故解答过程为:
88÷(3+1)+15=37(千克)
88-37=51(千克)
答:甲箱原有零件37个,乙箱原有零件51个。
5
例题 4
某畜牧场有山羊、绵羊共670只,如果绵羊减少30只,山羊增加200只,则山羊的只数就是绵羊的3倍。求原来山羊、绵羊各多少只?
分析:
依题意可知,绵羊减少30只,山羊增加200只,这时羊的总数为
670-30+200=840(只),而且山羊的只数是绵羊的3倍,就可求出此时绵羊有840÷(3+1)=210(只),那么原来绵羊有210+30=240(只),山羊有670-240=430(只)。
故解答过程为:
(670-30+200)÷(3+1)+30=240(只)
670-240=430(只)
答:原来山羊有430只,绵羊有240只。
6
练习题:
1、某小学买来足球和排球共36个,其中足球的个数是排球的个数的2倍。求该小学买来足球和排球各多少个?
2、一所小学共有学生868人,中年级的学生人数是高年级的2倍,低年级的学生人数是中年级的2倍。这所学校高、中、低年级各有学生多少人?
3、小明、小华两人共有糖果63块,如果小明给小华9块糖果,那么小华糖果的块数就是小明的2倍。他们两人原有糖果各多少块?
4、有两堆棋子共49个,如果第一堆增加15个,第二堆减少4个,则第二堆的个数是第一堆的2倍。求两堆棋子原来分别有多少个?
END差倍问题
1
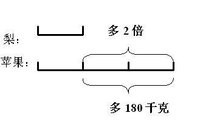
前面我们学习了解答和倍问题的方法,这里我们再来学习与和倍问题有相似之处的差倍问题。已知两数的差以及它们之间的倍数关系,求这两个数各是多少的应用题就叫做差倍问题。
基本思路:
差倍问题的解题关键,是确定“1倍数”和“差”是多少。
解题公式:
两数之差÷(倍数-1)=1倍数

2
例题 1
已知一支钢笔比一支圆珠笔贵4元,且钢笔的价钱正好是圆珠笔的3倍。问每支钢笔和每支圆珠笔各多少元?
分析:
把圆珠笔的单价看作1倍,那么4元就相当于圆珠笔单价的(3-1)倍。这样,把4元平均分成2份,1份就是圆珠笔的价钱,3份就是钢笔的价钱。
故解答过程为:
4÷(3-1)=2(元)
2×3=6(元)
答:每支钢笔6元,每支圆珠笔2元。
3
例题 2
四年级学生参加课外活动,跳绳的人数比打球人数的3倍多8人,且跳绳比打球的多64人。跳绳和打球的各有多少人?
分析:
把打球的人数看作1倍,那么跳绳的人数就是这样的3倍多8人。而(64-8)人正好相当于打球人数的2倍。因此,打球的人数是(64-8)÷(3-1)=28(人),跳绳的有28+64=92(人)。
故解答过程为:
(64-8)÷(3-1)=28(人)
28+64=92(人)
答:打球的有28人,跳绳的有92人。
4
例题 3
小明有存款5400元,小强有存款3800元。两人各取出同样多的钱后,小明的存款是小强的3倍。问:取款后两人各有存款多少元?
分析:
由于两人的取款数相同,所以,两人的存款差不变,还是相差
5400-3800=1600(元)。取钱后,小强的钱是1倍数,小明的钱就是3倍数,用差除以倍数之差就能得到1倍数,即小强取款后的钱数了。
故解答过程为:
(5400-3800)÷(3-1)=800(元)
800×3=2400(元)
答:取款后,小强有800元,小明有2400元。
5
例题 4
有两箱零件,如果从甲箱拿出18个放进乙箱,两箱的零件就同样多;如果从乙箱拿出13个放进甲箱,甲箱中的零件就是乙箱的3倍。甲、乙两箱原来各有零件多少个?
分析:
根据“从甲箱拿出18个放进乙箱,两箱的零件就同样多”可知,原来甲箱的零件比乙箱多18×2=36(个)。如果“从乙箱拿出13个放进甲箱”,这时,甲箱就比乙箱多36+13×2=62(个)零件。根据差倍问题的解题规律,乙箱里后来有零件62÷(3-1)=31(个),原来有31+13=44(个)。而甲箱里原来应该有44+36=80(个)零件。
故解答过程为:
(18×2+13×2)÷(3-1)+13=44(个)
44+18×2=80(个)
答:甲箱原来有80个零件,乙箱原来有44个零件。
6
练习题:
1、五年级参加跳绳比赛的女生人数是男生人数的3倍,且女生比男生多38人。参加跳绳比赛的男生和女生各有多少人?
2、果园里种了一批苹果树和桃树。已知苹果树比桃树多1800棵,且苹果树的棵数比桃树的3倍还多200棵。苹果树和桃树各有多少棵?
3、甲箱有零件45个,乙箱有零件25个。从两箱取出同样多的零件后,甲箱的零件数是乙箱的5倍。求后来两箱各有多少个零件?
4、甲、乙两仓都存有货物。若从甲仓取31吨放入乙仓,则两仓存货同样多;若从乙仓取14吨放入甲仓,则甲仓货物是乙仓的4倍。原来两仓各存货物多少吨?
END注意事项
解题要活学活用,多动脑思考。
做题要认真,不可马马虎虎、粗心大意!
温馨提示:经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。免责声明:本文转载来之互联网,不代表本网站的观点和立场。如果你觉得好欢迎分享此网址给你的朋友。转载请注明出处:https://www.baikejingyan.net/afa30VwdsBA5WAVMB.html

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 
