本文采用两种方法，一是利用角平分线、正弦定理与长度关系，二是利用角平分线、正弦定理与长度关系，介绍已知半圆的直径为AB，其长度为R=34，AC=28，AC是∠DAB的角平分线，求AD的长。

问题由来

1

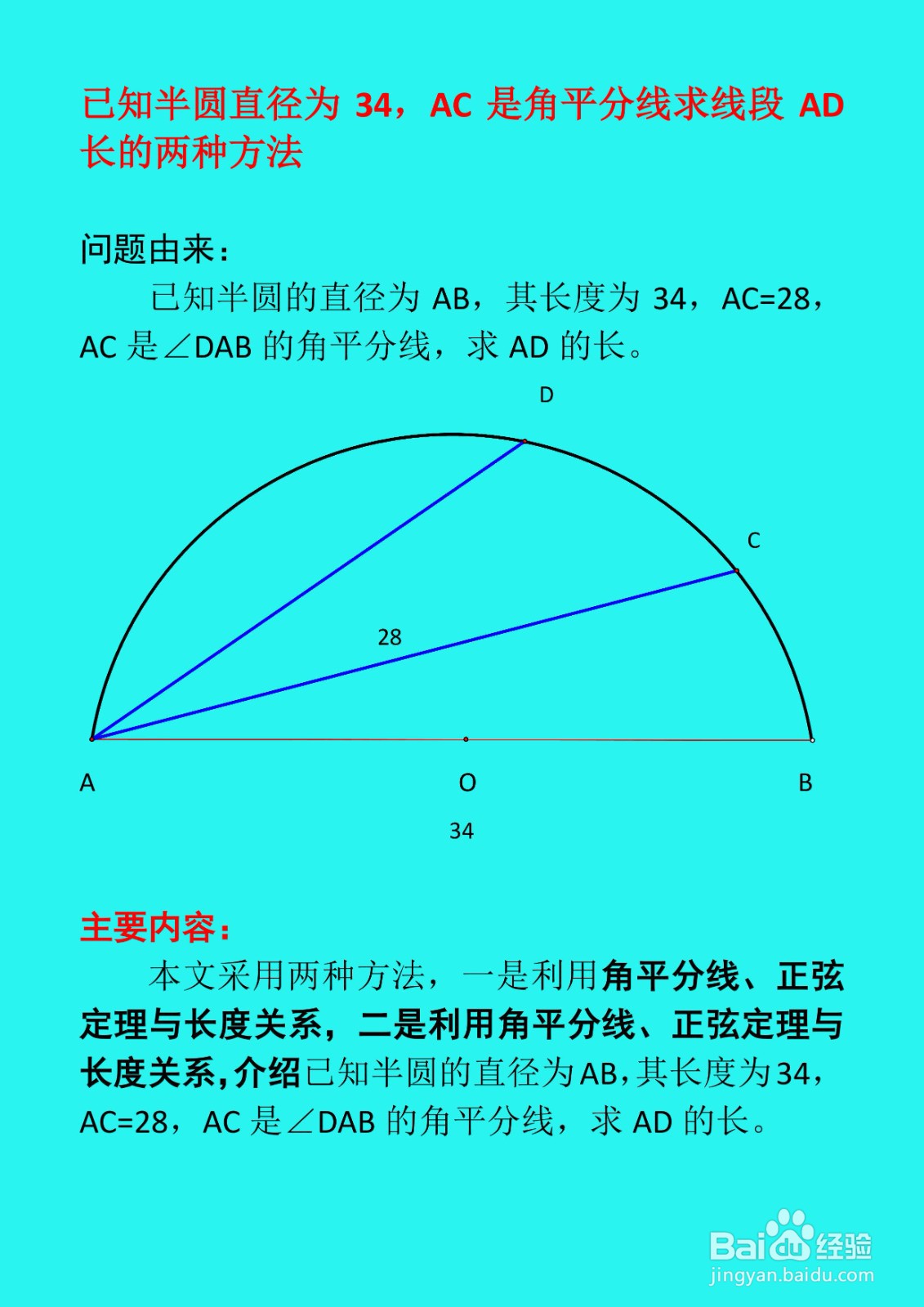
已知半圆的直径为AB，其长度为34，AC=28，AC是∠DAB的角平分线，求AD的长。

END

※.角度余弦值关系计算求解

1

[主要思路]：利用平分角a的余弦和其二倍角2a的余弦值关系来计算所求线段AD的长度。

设圆的半径为R，即R=AB/2=17,在△AOD中，AO=OD=R=17,



2

由余弦定理有：

AD=2AM=2*Rcos2a=2*17cos2a=34cos2a…….(1)

在三角形AOC中，由余弦定理有：

AC=2*AN=2*Rcosa=34*cosa,

即：34cosa=28,

所以：cosa=14/17.

代入方程(1)中，有：

AD=34cos2a=34*(2cos ²a-1),

=34*[2*(14/17) ²-1],

=206/17.

END

※.角平分线、正弦定理与长度关系来求解

1

[主要思路]：本步骤利用已知条件角平分线定理、正弦定理，并根据角a的余弦值，以及长度关系，来求解计算所求线段的长度。



2

如上图所示，设AD=x，OD与AC的交点为P，设DP=y，则OP=R-y，

即OP=17-y，在三角形△AOD中，AP是角平分线，由平分线定理可得：OP/PD=AO/AD,

则：(17-y)/y=R/x，化简为：

x=17y/(17-y),……(1).

进一步由正弦定理可得：

DP/sina=AD/sin∠APD,

即：y/sina=x/sin3a，化简为：y(3-4sin²a)=x,……(2),

在△AOC中，可求出cosa=14/17，



3

则：sin²a=93/289……(3),

将(3)代入(2)可知：

y=289x/495,

再代入(1)可知：

x=17*(289x/495)/[17-(289x/495)],

化简可得;

289x/495=17 *206/495,

所以：x=206/17.

END