一次函数是初中数学的一个重点内容，在现实生活中有着广泛的应用。它是一次方程（组）、一次不等式（组）的延伸，又是后续其他函数学习的开始。本章的内容主要有一次函数的概念、图像和性质，一次函数与一次方程、一次不等式的关系，综合应用函数的性质解决实际问题。主要有数形结合思想、转化思想、分类讨论思想、待定系数法等数学思想方法.

那么这篇文章我们就专门来学习——一次函数！

一、从概念出发，理解一次函数与正比例函数的关系

1

函数的概念：在某个变化过程中有两个变量，设为x和y，如果在变量x的允许取值范围内，变量y随着x的变化而变化，并且对于每一个x的值，y有唯一确定的值与之对应，那么变量y叫作变量x的函数，x叫作自变量。

2

一次函数的概念：

一般地，形如y=kx+b（k、b是常数，k≠0）的函数，叫作一次函数；

特别地，当b=0时，一次函数y=kx+b（k≠0）为y=kx（k≠0）是正比例函数。所以说正比例函数是一次函数的特例。

END

二、用数形结合，正确认识一次函数的图像

1

一次函数y=kx+b（k、b是常数，k≠0）的图像是一条直线。作图时通常取它与坐标轴的两个交点(0,b)、(-b/k,0)，即可画出一次函数的图像。

2

一次函数y=kx+b的图像可看作是由正比例函数y=kx的图像向上或向下平移得到.（如图1）当b＞0时，向上平移b个单位；当b＜0时，向下平移∣b∣个单位。



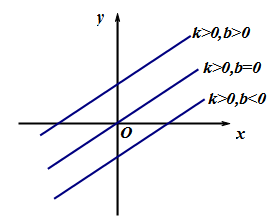
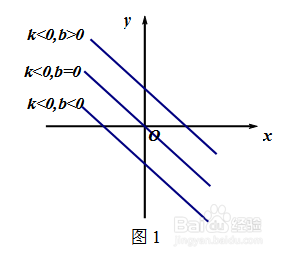
3

一次函数的图像由k、b共同决定，截距b决定了直线与y轴的交点，而k决定了直线相对于x轴正方向的倾斜程度.

END

三、用图形运动，灵活掌握一次函数的性质

1

正比例函数是特殊的一次函数，一次函数y=kx+b（k、b是常数，k≠0）的增减性与正比例函数是一致的，即：

（1）当k＞0时，函数值y随自变量x的值增大而增大；

（2）当k＜0时，函数值y随自变量x的值增大而增小.

2

一次函数y=kx+b（k、b是常数，k≠0）的图像可以看作是y=kx平移得到的，

（1）当k＞0，b=0时，图像y=kx经过第一、三象限；若b＞0，将y=kx向上平移，图像经过第一、二、三象限；若b＜0，将y=kx向下平移，则图像经过第一、三、四象限；

（2）当k＜0，b=0时，图像y=kx经过第二、四象限；若b＞0，将y=kx向上平移，图像经过第一、二、四象限；若b＜0，将y=kx向下平移，则图像经过第二、三、四象限.

END

四、用待定系数法，求一次函数解析式

1

求一次函数的解析式一般用待定系数法，解题步骤为“一设、二列、三解、四还原”.

一设：设出一次函数解析式的一般形式y=kx+b（k≠0）；

二列：根据已知两点或图像上两个点的坐标列出关于k、b的二元一次方程组；

三解：解这个方程组，求出k、b 的值；

四还原：将已求得的k、b代入解析式.

2

另外，对于求实际问题中的一次函数的解析式可仿照列方程解应用问题，但应注意自变量的取值范围应受实际条件的限制.

END

五、用一次函数的观点，看一次方程、不等式

1

1.一次函数和一元一次方程

对于方程 -2x+8=0的解是x=4；对于一次函数y=-2x+8，当函数y=-2x+8的值等于0时，函数自变量x=4. 由此，直线y=-2x+8与x轴的交点坐标（4，0）. （如图2）



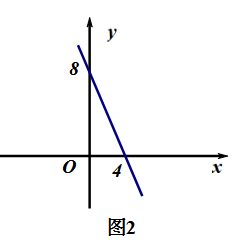
2

通过观察分析一次函数y=-2x+8的图像，也可以得到方程-2x+8=0的解是x=4. 由于任何一元一次方程都可以转化为ax+b=0(a,b为常数，a≠0)的形式，所以解一元一次方程可以转化为：当某个一次函数的值0时，求相应的自变量的值.从图像上看，这相当于已知直线y=ax+b，求它与轴x交点的横坐标的值.

3

2.一次函数与一元一次不等式

对于不等式2x-6＜0，即其解集为x＜3.而对于函数y=2x-6，当自变量x＜3时，函数y=2x-6的值小于0.

由此，我们可以通过图3，解不等式2x-6＜0与求当自变量为何值时，函数y=2x-6的值小于0是同一个问题，即当x＜3时，这条直线上的点在x轴的下方，此时有y=2x-6＜0.



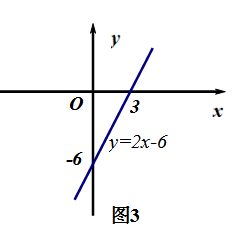
4

由于任何一元一次不等式都可以转化为ax+b＞0或ax+b＜0(a，b为常数，a≠0)的形式，所以解一元一次不等式可以看作：当一次函数值在大（小）于0时，求自变量相应的取值范围.

END

六、用函数思想，解决实际生活中的问题

1

学习了一次函数与正比例函数的一般形式和它们的图像、性质后，还要能运用一次函数的性质解决实际生活中的问题，从而体会函数建模思想，提高自己的解题能力.

接下来我们就来做做题练练吧！

2

例：某纺织厂生产的产品,原来每件出厂价为80元，成本为60元.由于在生产过程中平均每生产一件产品有 0.5 立方米的污水排出，现在为了保护环境，需对污水净化处理后再排出. 已知每处理1立方米污水的费用为2元，且每月排污设备损耗为 8000元.设现在该厂每月生产产品x件，每月纯利润y元.

（1）求y与x的函数关系式(纯利润=总收入－总支出)；

（2）当 = 106000 时，求该厂在这个月中生产产品的件数.

3

不要偷看哟~

不要偷看哟~

不要偷看哟~

不要偷看哟~

不要偷看哟~

不要偷看哟~

不要偷看哟~

END

七、练习题答案

1

解析：

（1）依题意得：

y=80x-60x-0.5x×2-8000，

y=19x-8000，

所以所求的函数关系式为y=19x-8000(x＞0且x是整数)；

（2）当y=106000 时，

x= 6000，

即这个月该厂生产产品6000件.

END

注意事项

一定要认真做笔记并仔细核对答案并反思哟~