通过三角形的三种面积计算方法,介绍已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18)三角形面积的主要步骤。
思路一:以边的长和高计算面积
1
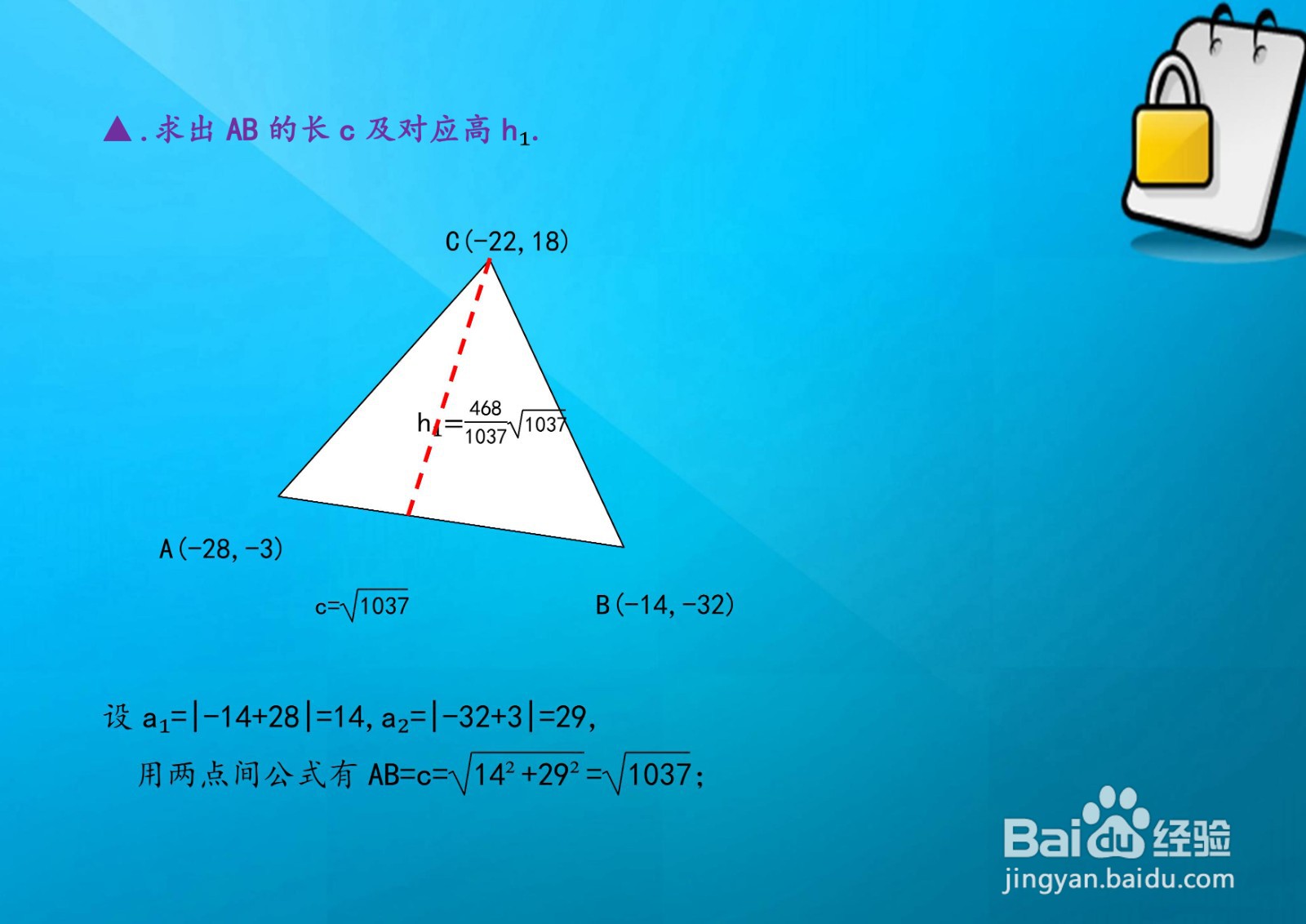
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),求出AB的长c及对应高h₁,再求三角形的面积。

2
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),计算出AB的长。
3
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),求出AC的长b及对应高h₂,进而求三角形的面积。

4
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),计算出AC的长。

5
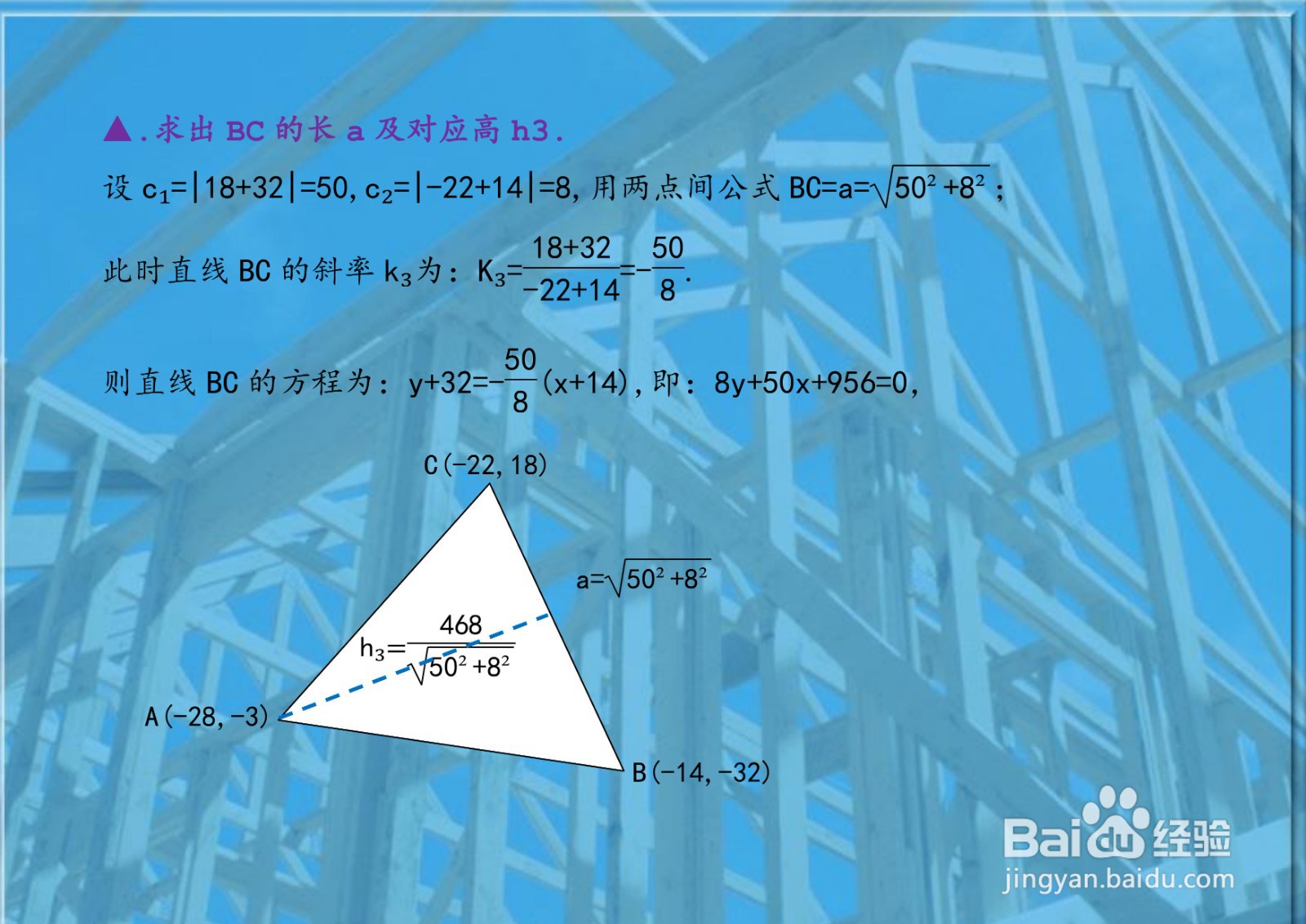
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),求出BC的长a及对应高h3,再求三角形ABC的面积。

6
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),解析边BC的直线方程。
7
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),此时三角形的面积算步骤如下:
 END
END思路二:向量计算面积
1
求出以其中一个点为端点的两个向量的模及其夹角,再利用三角形面积等于其中一个角的正弦值与该角相邻两边长度乘积的一半,即可计算出三角形的面积。

2
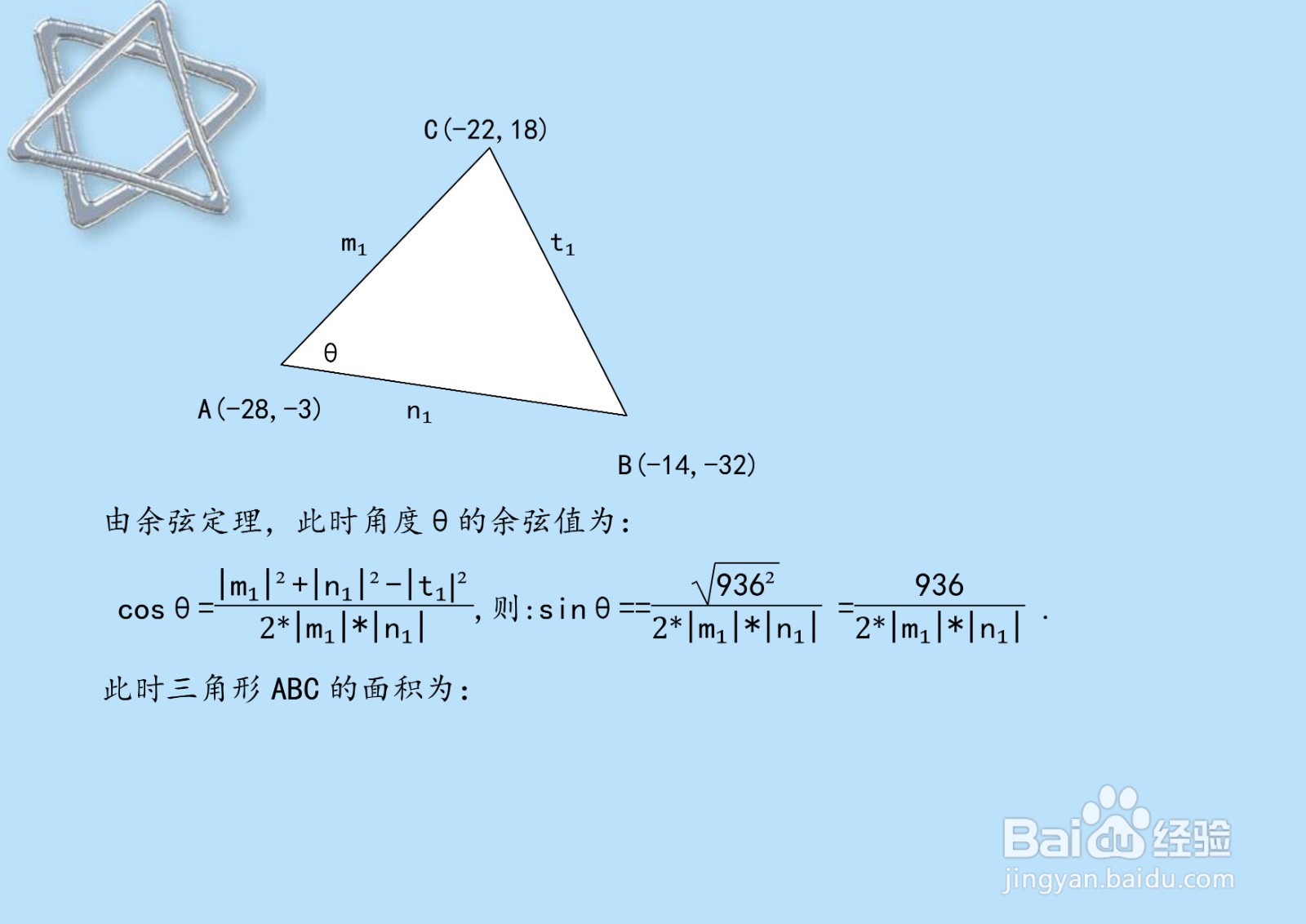
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),以角度A的夹角θ计算时,先求出余弦值cosθ,再计算正弦值sinθ。
3
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),根据公式S=*|m₁|*|n₁|*sinθ,即可计算三角形的面积。

4
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),以角度B的夹角α计算时,先求出余弦值cosα,再计算正弦值sinα。

5
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),根据公式S=*|t₁|*|n₁|*sinα,即可计算三角形的面积。
6
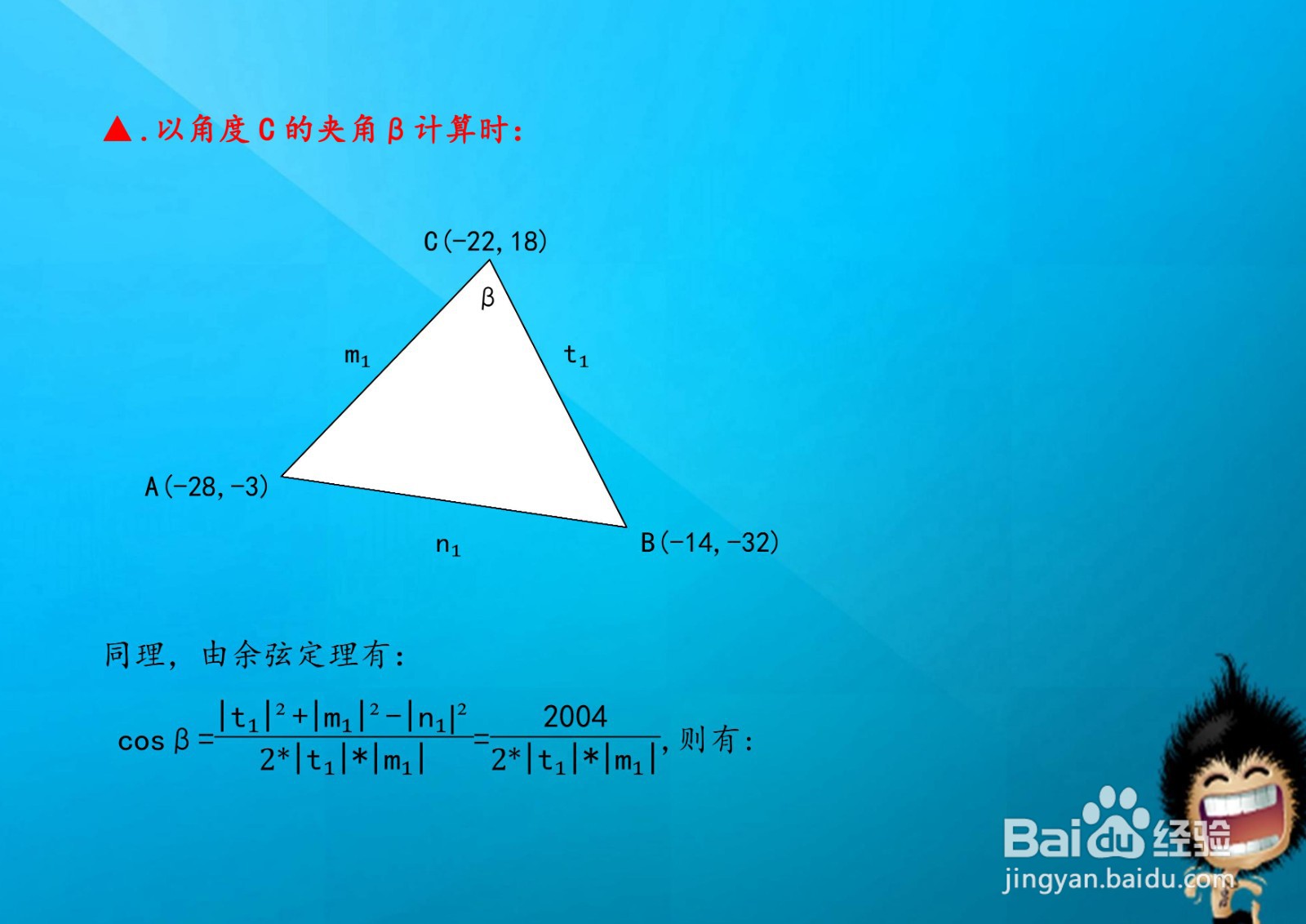
已知三角形的三个顶点坐标分别为A(-28,-3),B(-14,-32),C(-22,18),以角度C的夹角β计算时,先求出余弦值cosβ,再计算正弦值sinβ。
 END
END思路三:行列式计算面积
1
【主要思路】三角形三个顶点坐标为(x1,y1),(x₂,y₂),(x₃,y₃)。则行列式的值取绝对值再除2就是三角形的面积。
 END
END温馨提示:经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。免责声明:本文转载来之互联网,不代表本网站的观点和立场。如果你觉得好欢迎分享此网址给你的朋友。转载请注明出处:https://www.baikejingyan.net/af8a3VwdsBA5QBlQG.html

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 
