三角函数是一个重要的知识点,尤其在生活应用中具有举足轻重的作用!三角函数包括sin cos,tan,cot,以及arctan,arccos,等等。他们之间是如何换算的?他们之间又有什么特殊的关系式子?
定义表达式
1
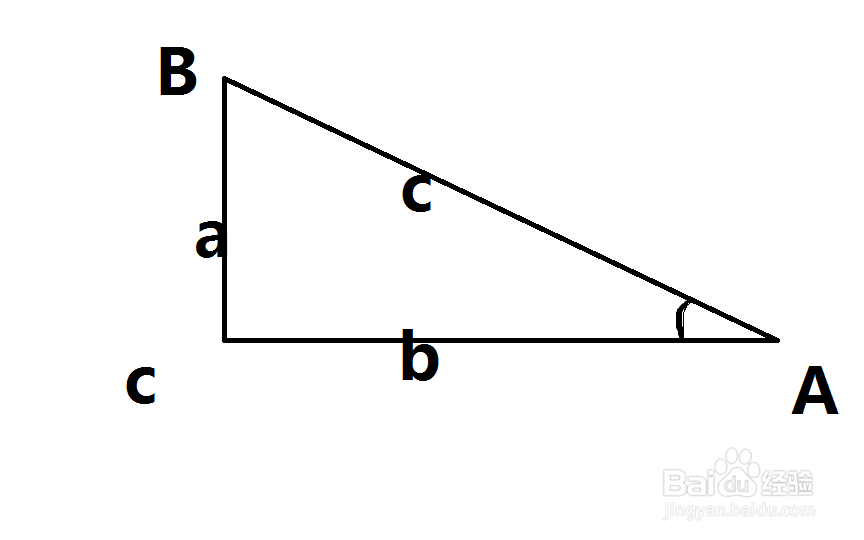
直角三角函数的定义:
正弦(sin)等于对边比斜边;sinA=a/c ;
余弦(cos)等于邻边比斜边;cosA=b/c ;
正切(tan)等于对边比邻边;tanA=a/b ;
余切(cot)等于邻边比对边;cotA=b/a;
一般在解三角形中经常使用这些等式!
2
倒数关系:
tanα ·cotα=1;
sinα ·cscα=1;
cosα ·secα=1 ;
这些等式可以直接由定义式子直接算出来,这里的角度α是任意的。

3
商的关系:
sinα/cosα=tanα=secα/cscα ;cosα/sinα=cotα=cscα/secα ;

4
平方关系:sin^2(α)+cos^2(α)=1 ;
1+tan^2(α)=sec^2(α) ;
1+cot^2(α)=csc^2(α) ;

5
二倍角公式
正弦 sin2α=2sinα·cosα ;
余弦 1.Cos2α=Cos^2(α)-Sin^2(α) ;
2.Cos2α=1-2Sin^2(α) ;
3.Cos2α=2Cos^2(α)-1 ;
即Cos2α=Cos^2(α)-Sin^2(α)=2Cos^2(α)-1=1-2Sin^2(α);正切tan2α=(2tanα)/(1-tan^2(α));
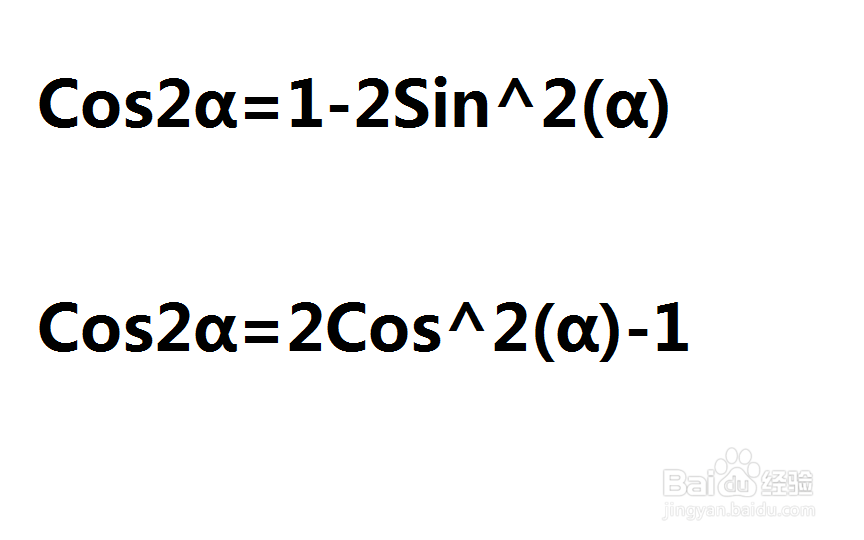 END
END不常用的关系式
1
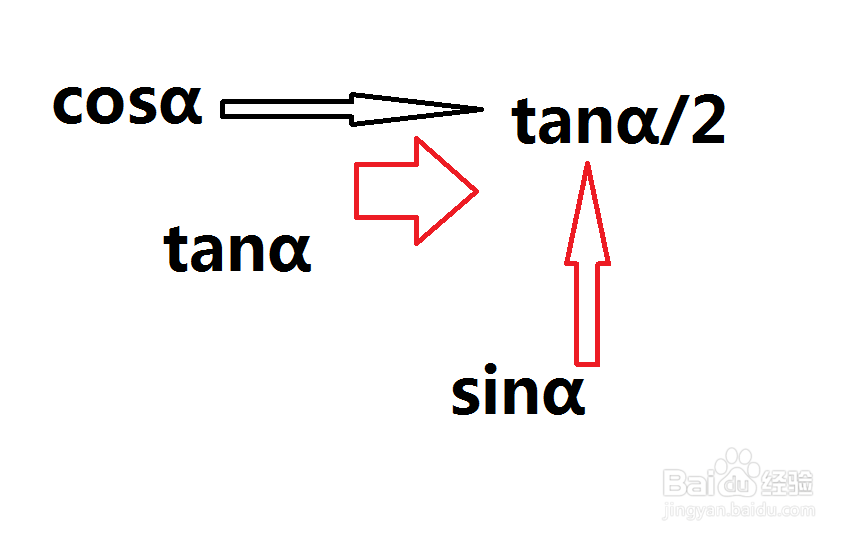
万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)] ;
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] ;
tanα=2tan(α/2)/[1-tan^2(α/2)];
建立了sinα,cosα,tanα与tanα/2 之间的关系。
2
半角公式
tan(α/2)=(1-cosα)/sinα=sinα/(1+cosα);
cot(α/2)=sinα/(1-cosα)=(1+cosα)/sinα;
sin^2(α/2)=(1-cos(α))/2;
cos^2(α/2)=(1+cos(α))/2;
tan(α/2)=(1-cos(α))/sin(α)=sin(α)/(1+cos(α)) ;
建立了半角与正个角之间的转化关系。
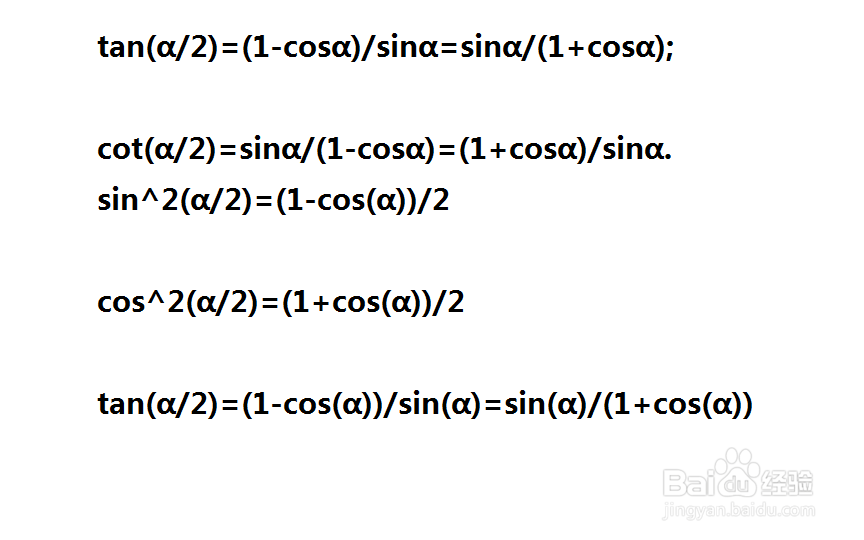
3
和差化积 sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2];
sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2];
cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2];
cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2];
tanθ+tanφ=sin(θ+φ)/cosθcosφ=tan(θ+φ)(1-tanθtanφ);
tanθ-tanφ=sin(θ-φ)/cosθcosφ=tan(θ-φ)(1+tanθtanφ)
将三角函数的额和,化成乘积的形式。

4
两角和公式 tan(α+β)=(tanα+tanβ)/(1-tanαtanβ);
tan(α-β)=(tanα-tanβ)/(1+tanαtanβ);
cos(α+β)=cosαcosβ-sinαsinβ;
cos(α-β)=cosαcosβ+sinαsinβ;
sin(α+β)=sinαcosβ+cosαsinβ;
sin(α-β)=sinαcosβ -cosαsinβ
将一个角度拆成两个角之和或者差的形式

5
积化和差 sinαsinβ =-[cos(α+β)-cos(α-β)] /2;
cosαcosβ = [cos(α+β)+cos(α-β)]/2;
sinαcosβ = [sin(α+β)+sin(α-β)]/2;
cosαsinβ = [sin(α+β)-sin(α-β)]/2;

6
三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α);
cos3α=4cosα·cos(π/3+α)cos(π/3-α);
tan3a = tan a · tan(π/3+a)· tan(π/3-a);
不常用,了解一下。
7
四倍角公式
sin4A=-4*(cosA*sinA*(2*sinA^2-1)) cos4A=1+(-8*cosA^2+8*cosA^4) tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)
不常用,了解一下。
8
五倍角公式
sin5A=16sinA^5-20sinA^3+5sinA cos5A=16cosA^5-20cosA^3+5cosA tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)
不常用,了解一下。
END注意事项
有问题输入错误,请回复随时修改!
温馨提示:经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。免责声明:本文转载来之互联网,不代表本网站的观点和立场。如果你觉得好欢迎分享此网址给你的朋友。转载请注明出处:https://www.baikejingyan.net/afabaU28CDABQB1Q.html

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 
